배열에서 특정 값을 찾는 가장 쉬운 방법은 배열의 맨 앞에서부터 차례대로 찾아나가는 방법입니다. 이는 순차 탐색(Sequential Search) 혹은 선형 탐색(Linear Search)이라고 하며 최대 n개의 원소들을 확인해야 하므로 O(n)의 시간복잡도를 가집니다.
하지만 배열이 오름 차순이나 내림 차순으로 정렬되어 있음이 보장된다면, 이 정보를 활용해 특정 값을 더 빠르게 찾을 수 있습니다. 예를 들어, 오름 차순으로 정렬된 A = [?, ?, ?, 16, ?, ?, ?] 라는 배열이 존재할 때, 15라는 값이 배열 내 몇 번째에 존재하는지 찾고자 한다고 가정할게요. 이 때, 배열의 3번 인덱스 즉, index = 3을 탐색했을 때, A[3] = 16입니다. 그럼 우리가 찾고 싶은 15라는 값은 적어도 index = 3보다 작은 위치에 존재할 것입니다. 그 다음 0 ~3의 중간값인 index = 1을 탐색했을 때, A[1] = 6이라면 A[2]는 6 ~ 16 사이의 값을 가지고 있다는 것을 확신할 수 있죠. 물론 그 값이 15인지 아닌지는 직접 탐색하기 전까지는 알 수 없지만요.
이처럼 정렬된 배열을 절반으로 나누어 찾고자 하는 값이 존재하는 범위를 찾아 탐색하는 방식을 이분 탐색(Binary Search) 혹은 이진 탐색이라고 합니다. n개의 원소로 이루어진 배열을 절반으로 나눈 뒤, 찾고자 하는 값이 왼쪽 배열, 오른쪽 배열 중 어디 있는지 찾아나가면 되기 때문에 시간복잡도는 O(log n)입니다. n = 2⁹⁹⁹⁹⁹ 처럼 큰 배열도 99,999번만 탐색하면 찾을 수 있는 획기적인 방법이에요.
자바는 배열 관련 클래스 Arrays의 Arrays.binarySearch() 메소드, 자료 구조 관련 클래스 Collections의 Collections.binarySearch() 메소드로 이분 탐색을 제공합니다. 특히 Collections에서 제공하는 이분 탐색 메소드가 재미있게 구현되어 있어 이 포스트를 작성하는 동기가 되었습니다. 그럼 Arrays.binarySearch() 부터 알아봅시다!
Arrays 클래스는 java.util 패키지의 일부로, 배열을 다루기 위한 다양한 메소드를 제공합니다. 이분 탐색 뿐만 아니라 배열을 정렬하는 Arrays.sort() 메소드, 배열을 특정 값으로 채우는 Arrays.fill() 메소드, 배열을 복사하는 Arrays.copyOf() 메소드 등도 말이죠. 특히 배열을 정렬하는 메소드 구현이 재미있는데, 이건 추후에 다른 포스트에서 소개하겠습니다.
Arrays 클래스에서 주목할 만한 또 다른 점은 boolean을 제외한 int, long, short, char, byte, double, float 와 같은 원시 타입 배열에 대해서 각각 메소드가 구현되어 있다는 점입니다. 즉, 동일한 이름의 메소드 sort, fill, copyOf, binarySearch 등에 대해서 매개변수 타입에 따라 오버로딩되어 있습니다.
JDK 17버전을 사용했습니다. 대표적으로 long 타입에 대한 Arrays.binarySearch()의 구현을 보도록 할게요. 나머지 타입도 구현은 같습니다.
// /java.base/util/Arrays.java
// ...
static void rangeCheck(int arrayLength, int fromIndex, int toIndex) {
if (fromIndex > toIndex) {
throw new IllegalArgumentException(
"fromIndex(" + fromIndex + ") > toIndex(" + toIndex + ")");
}
if (fromIndex < 0) {
throw new ArrayIndexOutOfBoundsException(fromIndex);
}
if (toIndex > arrayLength) {
throw new ArrayIndexOutOfBoundsException(toIndex);
}
}
// ...
public static int binarySearch(long[] a, long key) {
return binarySearch0(a, 0, a.length, key);
}
public static int binarySearch(long[] a, int fromIndex, int toIndex, long key) {
rangeCheck(a.length, fromIndex, toIndex);
return binarySearch0(a, fromIndex, toIndex, key);
}
// Like public version, but without range checks.
private static int binarySearch0(long[] a, int fromIndex, int toIndex, long key) {
int low = fromIndex;
int high = toIndex - 1;
while (low <= high) {
int mid = (low + high) >>> 1;
long midVal = a[mid];
if (midVal < key)
low = mid + 1;
else if (midVal > key)
high = mid - 1;
else
return mid; // key found
}
return -(low + 1); // key not found.
}
// ...Arrays.binarySearch()와 관계된 메소드는 이렇게 4개의 메소드입니다. 여기서 실제 호출할 수 있는 건 전체 배열 범위에 대해서 key의 index를 찾는 binarySearch(long[] a, long key)와 fromIndex부터 toIndex 범위에서 key의 index를 찾는 binarySearch(long[] a, int fromIndex, int toIndex, long key)입니다. 그럼 차례대로 하나씩 알아볼게요.
rangeCheck()는 Arrays 클래스 전반에 걸쳐 매개변수 유효성 검증의 책임을 가지고 있는 헬퍼 메소드입니다. 코드를 보면 크게 세 가지 경우에 따라 예외를 던지는 것을 알 수 있습니다.
•
fromIndex > toIndex : 시작 인덱스가 끝 인덱스보다 큰 경우
•
fromIndex < 0 : 시작 인덱스가 0보다 작을 경우
•
toIndex > arrayLength : 끝 인덱스가 배열의 크기보다 큰 경우
가장 많이 호출하는 메소드입니다. 내부적으로는 전체 범위를 검색하는 binarySearch(a, 0, a.length, key)를 호출합니다.
배열 a의 특정 범위에 대해 이분 탐색을 수행하는 메소드입니다.
•
매개변수 fromIndex와 toIndex에 대해서 유효한지 확인하는 rangeCheck() 메소드를 호출
•
문제가 없을 경우 binarySearch0(long[] a, int fromIndex, int toIndex, long key)를 호출
여기서 실제 이분 탐색을 수행하고 인덱스를 리턴합니다. 이분 탐색을 그대로 구현한 코드지만, 몇 가지 특징이 있습니다.
int low = fromIndex;
int high = toIndex - 1;toIndex - 1을 해서 toIndex는 탐색 범위에 들어가지 않습니다.(Exclusive)
int mid = (low + high) >>> 1;low와 high의 중간 인덱스를 찾을 때, 저는 보통 그냥 나누기 2를 하는데, 자바 구현에서는 쉬프트 연산자를 사용해서 비트를 오른쪽으로 한 칸 이동시키는 최적화가 있었습니다. 결과는 같지만, CPU의 부하를 조금이나마 줄일 수 있겠네요.
return -(low + 1); // key not found.이 부분이 재미있는 점입니다.
Arrays.binarySearch() 메소드는 값을 찾지 못했을 때, 음수 값을 리턴합니다. 그리고 이 값은 랜덤한 값이 아니라 탐색에 실패했을 때 하나의 리턴값으로 한 번에 두 가지 목적을 달성하기 위한 효율적인 설계입니다. 두 가지 목적은 다음과 같습니다.
•
검색에 실패했다.
•
배열을 정렬된 상태로 유지하려면 이 위치에 삽입해야 한다. (Insertion Point를 알려줌)
예를 들겠습니다. A = [1, 3, 5, 7]일 때, key = 4를 찾는다고 가정하면 Arrays.binarySearch(A, 4)에서 탐색에 실패하고 -3을 리턴합니다. 이 값이 음수이므로 우리는 탐색에 실패했음을 알 수 있겠죠. 그리고 key = 4를 배열에 삽입해야 한다면, -(result + 1) 즉 -(-3 + 1) = 2인 위치에 삽입하면 됩니다. A = [1, 3, 4, 5, 7]가 자연스럽죠.
그럼 당연히 또 하나의 의문이 듭니다. 왜 -(result + 1)인가? 그것은 바로 Insertion Point가 0일 때 모호함을 구별하기 위함입니다. 이분 탐색한 뒤 0이란 값을 리턴 받았다면, 이 값이 검색에 성공해서 0번 인덱스에 해당 값이 있다는 뜻인지, 없으니까 0번 인덱스에 값을 삽입하면 된다는 뜻인지 알 수 없습니다. 이러한 혼란을 피하기 위해서 자바에서는 탐색에 실패했을 경우 - (Insertion Point + 1)를 반환합니다.
이처럼 하나의 리턴 값으로 두 개의 정보를 얻을 수 있는 구현은 Collections 클래스에서도 마찬가지입니다. 이제 Collections.binarySearch() 메소드에 대해 알아봅시다.
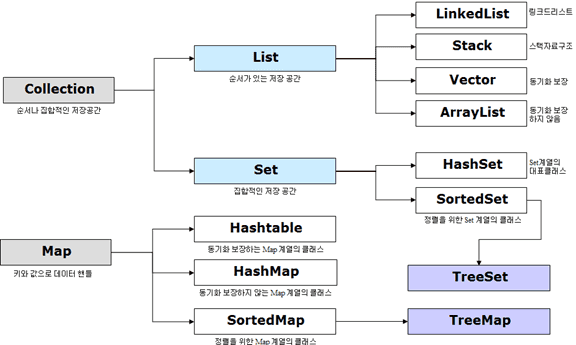
Java Collections Framework
Collections 클래스 또한 java.util 패키지의 일부로, 다양한 Collection을 다루기 위한 수많은 메소드를 제공합니다. 자바는 Java Collections Framework(JCF)라는 이름으로 많은 데이터를 효율적으로 관리하기 위한 자료 구조를 제공하며, 자료 구조를 구현한 클래스와 인터페이스 집합을 제공합니다.
List, Set, Map 등등 다양한 인터페이스를 다룰 수 있는 수많은 메소드들이 있지만 그 중에서 Collections.binarySearch() 메소드와 관련한 코드를 알아보겠습니다.
Collections.binarySearch() 메소드와 관련된 코드 조각들은 아래와 같습니다. Collections 클래스에는 매개변수에 객체를 비교하기 위한 Comparator를 같이 넘겨주거나 없는 경우에 따라서 2개의 오버로드된 binarySearch() 메소드가 구현되어 있지만, 편의 상 Comparator를 같이 넘겨 주는 경우만 확인해보겠습니다.
// /java.base/util/Collections.java
// ...
private static final int BINARYSEARCH_THRESHOLD = 5000;
// ...
public static <T> int binarySearch(List<? extends T> list, T key, Comparator<? super T> c) {
if (c==null)
return binarySearch((List<? extends Comparable<? super T>>) list, key);
if (list instanceof RandomAccess || list.size()<BINARYSEARCH_THRESHOLD)
return Collections.indexedBinarySearch(list, key, c);
else
return Collections.iteratorBinarySearch(list, key, c);
}
private static <T> int indexedBinarySearch(List<? extends T> l, T key, Comparator<? super T> c) {
int low = 0;
int high = l.size()-1;
while (low <= high) {
int mid = (low + high) >>> 1;
T midVal = l.get(mid);
int cmp = c.compare(midVal, key);
if (cmp < 0)
low = mid + 1;
else if (cmp > 0)
high = mid - 1;
else
return mid; // key found
}
return -(low + 1); // key not found
}
private static <T> int iteratorBinarySearch(List<? extends T> l, T key, Comparator<? super T> c) {
int low = 0;
int high = l.size()-1;
ListIterator<? extends T> i = l.listIterator();
while (low <= high) {
int mid = (low + high) >>> 1;
T midVal = get(i, mid);
int cmp = c.compare(midVal, key);
if (cmp < 0)
low = mid + 1;
else if (cmp > 0)
high = mid - 1;
else
return mid; // key found
}
return -(low + 1); // key not found
}
private static <T> T get(ListIterator<? extends T> i, int index) {
T obj = null;
int pos = i.nextIndex();
if (pos <= index) {
do {
obj = i.next();
} while (pos++ < index);
} else {
do {
obj = i.previous();
} while (--pos > index);
}
return obj;
}
// ...관련된 코드는 크게 1개의 정적 변수 BINARYSEARCH_THRESHOLD와 호출하기 위한 binarySearch() 메소드, 그리고 분기에 따라서 호출되는 indexedBinarySearch() 메소드와 iteratorBinarySearch() 메소드가 있습니다. 추가적으로 iteratorBinarySearch()에서 내부적으로 사용하는 get() 메소드도 있습니다. 먼저 호출할 때 사용하는 binarySearch() 메소드부터 알아보겠습니다.
짧은 코드지만 재미있는 점이 많습니다.
if (c==null)
return binarySearch((List<? extends Comparable<? super T>>) list, key);매개변수 c가 null일 경우, 매개변수 list에 들어온 구현체가 이미 Comparable 인터페이스를 상속받아 구현했다고 가정하고 오버로드된 다른 메소드인 binarySearch((List<? extends Comparable<? super T>>) list, key)로 위임합니다. 만약 구현되어 있지 않다면, ClassCastException 예외가 발생합니다.
if (list instanceof RandomAccess || list.size()<BINARYSEARCH_THRESHOLD)
return Collections.indexedBinarySearch(list, key, c);
else
return Collections.iteratorBinarySearch(list, key, c);이제 경우에 따라 다른 메소드를 호출하는데 그 경우는 다음과 같습니다.
•
리스트 list 가 RandomAccess 인터페이스를 구현하거나 리스트의 크기가 BINARYSEARCH_THRESHOLD보다 작은 경우 → indexedBinarySearch() 호출
•
리스트 list 가 LinkedList처럼 순차 접근만 가능하고 리스트의 크기가 BINARYSEARCH_THRESHOLD보다 큰 경우 → iteratorBinarySearch() 호출
이 부분이 재밌는데, 임의 접근(Random Access) 여부와 리스트 크기에 따라서 서로 다른 메소드가 호출됩니다.
먼저, 임의 접근 여부에 따라서 다른 메서드가 호출되는 것은 이해하기 쉽습니다. ArrayList, Vector처럼 RandomAccess 인터페이스를 구현한 클래스의 경우 중간 인덱스에 접근할 때, get(index) 메소드를 사용하면 O(1)의 시간이 걸리기 때문에 매우 적절한 방법입니다. 반대로 임의 접근이 불가능한 LinkedList같은 경우에는 중간 인덱스에 접근하려면 head에서부터 순차적으로 접근해야 합니다. 따라서 O(n)의 시간복잡도가 걸리겠죠.
하지만, 임의 접근이 불가능한 LinkedList의 경우에도 리스트의 크기가 BINARYSEARCH_THRESHOLD보다 작다면 indexBinarySearch() 메소드를 사용합니다. 이 부분은 이상하지만 하나씩 뜯어보면 일리가 있습니다.
이를 이해하기 위해서는 LinkedList의 get() 메소드 동작 방식과 listIterator()에 대해서 알아야 합니다. LinkedList에서 get() 메소드를 이해하기 위한 코드를 확인해봅시다.
// java.base/util/LinkedList.java
// ...
Node<E> node(int index) {
// assert isElementIndex(index);
if (index < (size >> 1)) {
Node<E> x = first;
for (int i = 0; i < index; i++)
x = x.next;
return x;
} else {
Node<E> x = last;
for (int i = size - 1; i > index; i--)
x = x.prev;
return x;
}
}
// ...
public E get(int index) {
checkElementIndex(index);
return node(index).item;
}
// ...자바의 LinkedList는 DoublyLinkedList로 구현되어 있습니다. 즉, 양끝의 first와 last 노드를 가리키고 있고, 노드는 next 노드와 prev 노드를 가리키고 있어서 양쪽으로 이동할 수 있는 형태겠죠.
아래의 get() 메소드는 내부적으로 node(index).item을 리턴합니다. 그리고 node() 메소드를 보면 index가 LinkedList 크기의 절반보다 작을 때는 first에서 탐색을 시작하고, 클 때는 last에서 탐색을 시작해서 index 위치의 노드를 리턴합니다. 더 가까운 방향에서 시작하는 합리적인 방법이죠.
다음으로 ListIterator는 ArrayList, LinkedList, Vector처럼 객체들끼리 연결되어 있는 자료구조에 구현되어 있는 서브 클래스입니다. 특징으로는 연결된 객체들을 이동해 필요한 노드를 찾아 리턴한 뒤에도 사라지지 않고 해당 노드를 가리키고 있습니다. 따라서 재사용이 가능하다는 장점이 있습니다.
따라서 LinkedList의 크기가 어느정도 크다면 first나 last에서 탐색을 시작하는 것보다 ListIterator를 재사용해서 해당 위치부터 다음 탐색 위치를 찾는 게 더 빠를 수 있습니다.
그리고 주석에 따르면 그 경험적인 임계값이 BINARYSEARCH_THRESHOLD값인 5,000입니다.
BINARYSEARCH_THRESHOLD 값이 5,000 인 것이 과연 타당한지 알고 싶어졌습니다. 그래서 리스트의 크기에 따른 ArrayList의 이분 탐색 시간과 indexed, iterator를 이용한 LinkedList의 이분 탐색 시간을 벤치 마크했습니다. 각각 50번 무작위 값을 검색했습니다.
Size | ArrayList (ms) | LinkedList - indexed (ms) | LinkedList - iterator (ms)
------------------------------------------------------------------------------------------------------
50 | 0.084 | 0.119 | 0.614
500 | 0.117 | 0.301 | 0.517
1000 | 0.041 | 0.214 | 0.422
2000 | 0.027 | 0.717 | 0.511
3000 | 0.017 | 1.527 | 0.679
4000 | 0.028 | 1.587 | 1.793
5000 | 0.015 | 0.838 | 2.328
6000 | 0.025 | 1.097 | 1.978
50000 | 0.032 | 12.779 | 4.176
500000 | 0.096 | 262.199 | 68.989
5000000 | 0.087 | 7012.631 | 1500.095 결과를 보면 ArrayList는 임의 접근이 가능하기 때문에 크기에 따른 차이가 크지 않았지만, LinkedList의 경우에는 달랐습니다. Size가 2000보다 작을 때는 indexed를 이용한 이분 탐색 시간이 더 빨랐지만, 2000 이상에서는 iterator를 이용한 이분 탐색 시간이 더 빨라지기 시작했습니다.
제 컴퓨터로 진행한 벤치마크 결과는 자바가 정한 값과 상이했습니다.
물론, CPU나 기타 하드웨어적인 차이나 벤치 마크 방법 등에 의해 결과는 달라질 수도 있습니다. WORA를 슬로건으로 하는 자바인만큼 사양이 낮은 장비들도 포괄할 수 있는 보수적인 수치를 정한 것일 수도 있습니다.
굳이 왜 5,000이라는 값을 임계값으로 정했는지 관련 주석 말고는 개발자의 의도를 알 수 있는 방법은 없었습니다. 하지만 15년 전 Openjdk Repository에도 변함없이 5,000인 것을 발견했어요 15년 동안 하드웨어가 크게 발전한 만큼 이 값도 어느정도 수정될 필요가 있지 않을까요?!
Loading comments...
0
0
