Traveling Salesman Problem (외판원 문제)

v1 개정 2025.02.03

2025.01.20

· Updated 2025.02.03

외판원 문제란?

외판원 문제(Traveling Salesman Problem; TSP)는 컴퓨터 과학 및 수학 분야에서 잘 알려진 조합 최적화 문제입니다. 이 문제의 핵심은 주어진 각 도시(노드)를 정확히 한 번만 방문하고 시작 도시로 돌아가는 가능한 최단 경로를 찾는 것입니다. 이때, A도시에서 B도시로 가는 거리(d)는 가중치가 존재합니다. 문제의 경우에 따라서 시작점으로 돌아가지 않을 수도 있는데, 이 제약 조건이 없다고 해도 계산 복잡도는 변하지 않습니다.

어쨌든 TSP는 대표적인 NP-난해(NP-hard) 문제로 모든 문제에 대해서 다항식 시간에 해결할 수 있는 알려진 알고리즘은 없습니다. 대신 작은 N의 경우(일반적으로 N ≤ 16)에는 분기한정법(Branch and Bound; B&B; 가지치기)이나 DP로 풀 수 있습니다. 또, N이 큰 경우에는 1.5의 근사비를 가지는 크리스토피데스 알고리즘과 같은 근사 알고리즘으로 풀 수 있습니다.

외판원 문제는 택배 기사님들의 효율적인 방문 순서나 회로 기판를 만드는 기계의 효율적인 이동과 같이 현실에서 적용될 수 있습니다. 이러한 경우 N의 크기가 커질 수 있기 때문에 근사 알고리즘을 사용합니다. 정확한 답은 아니더라도 결과를 빠르게 낼 수 있다면 택배 기사님들이 한 두번 비효율적인 경로로 가시더라도 화내시지는 않겠죠?

문제 풀기

외판원 순회의 일반적인 문제를 가지고 한번 개선해 가면서 문제를 풀어보겠습니다. 풀 문제는 다음과 같습니다. 외판원 순회(백준 2098)

Approach A. 완전탐색(DFS)

설명

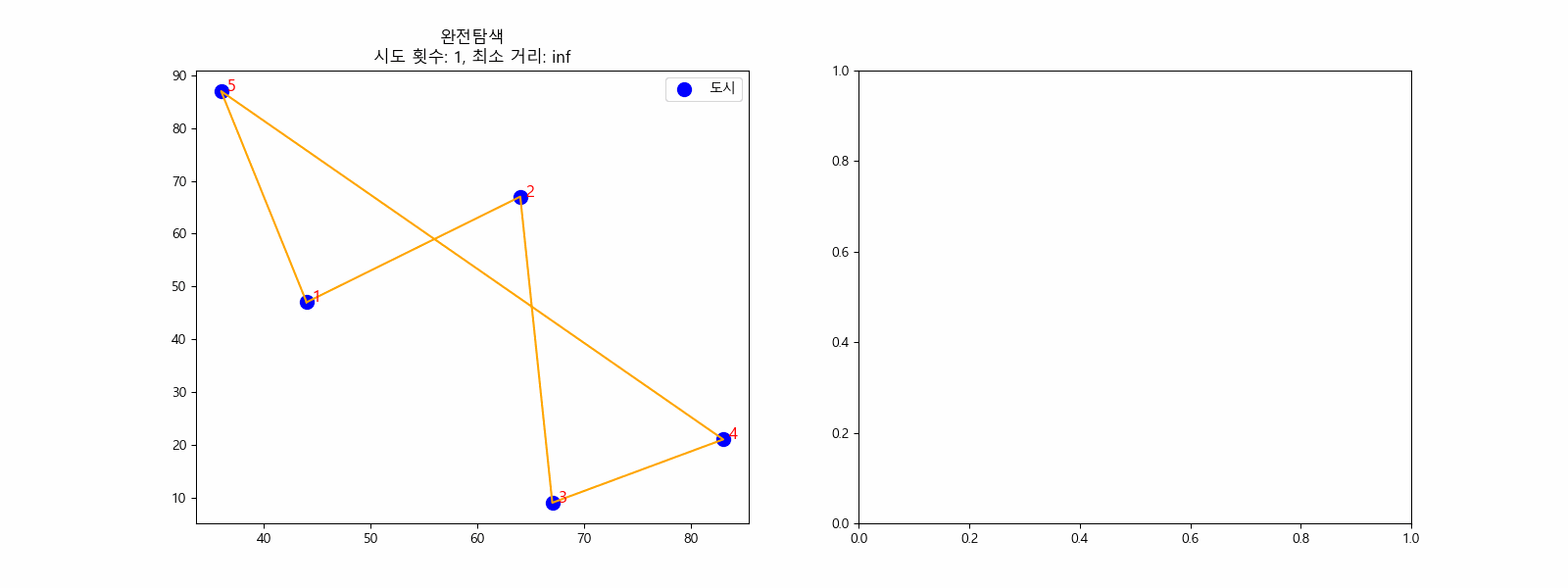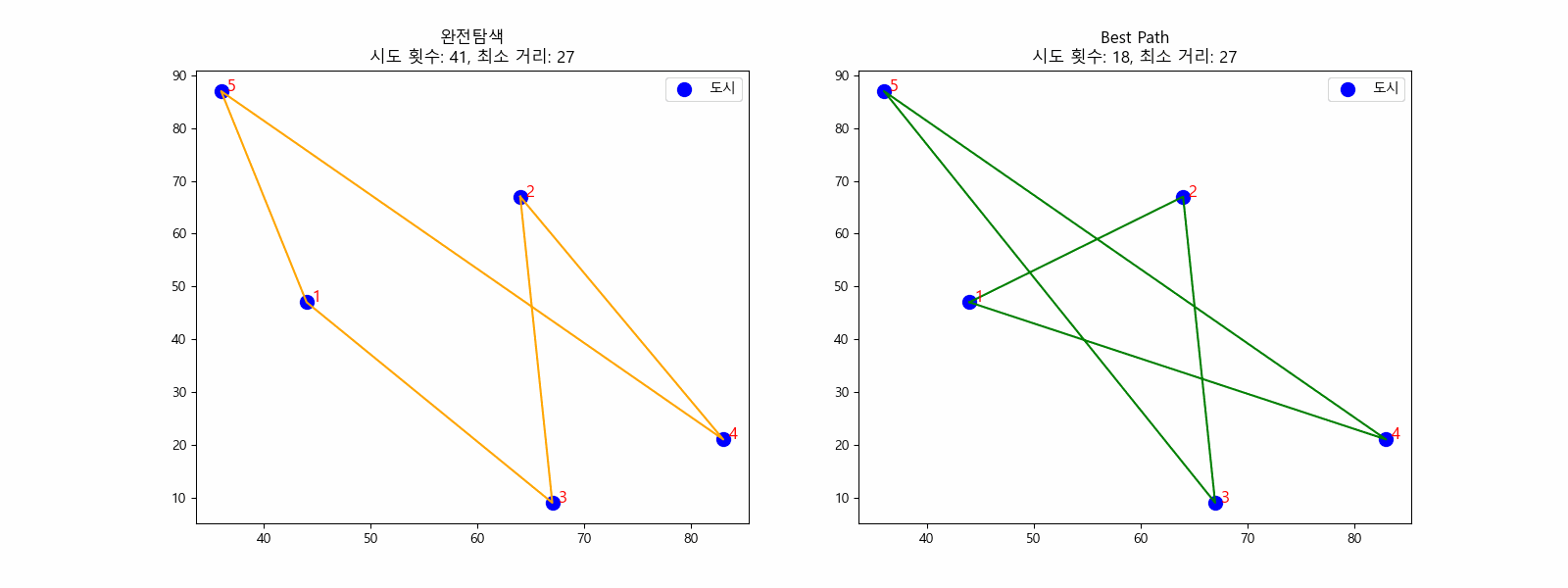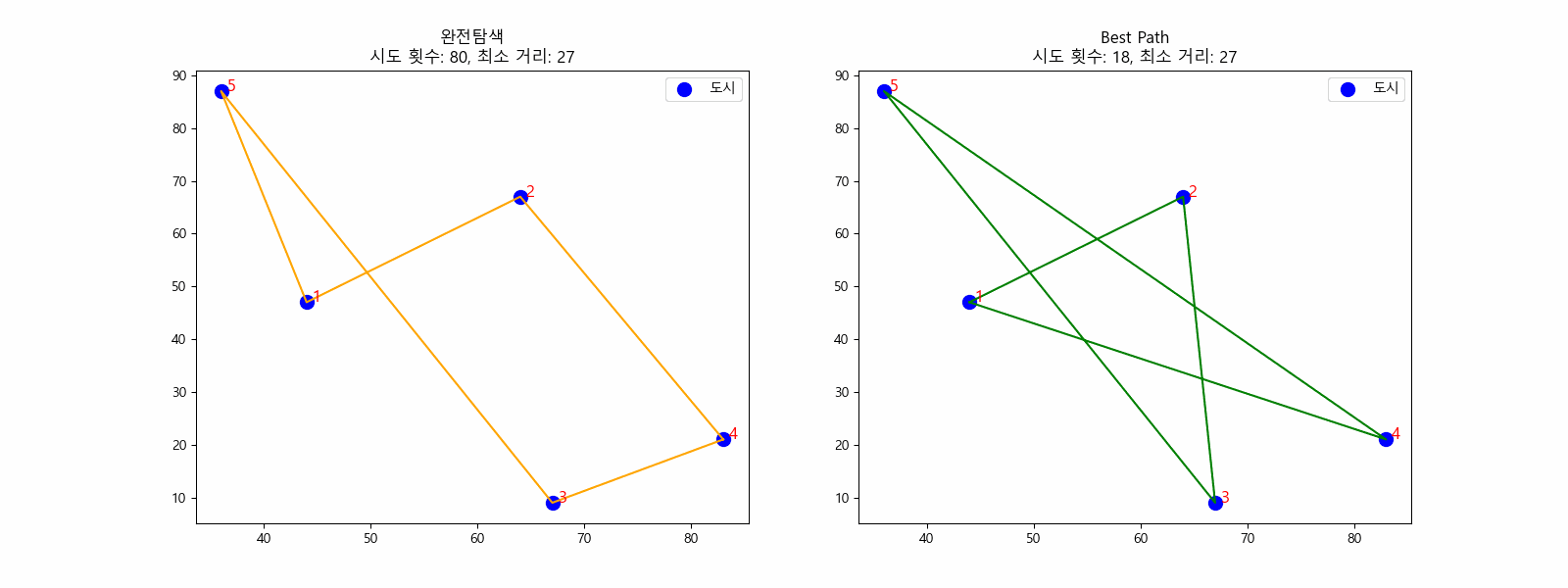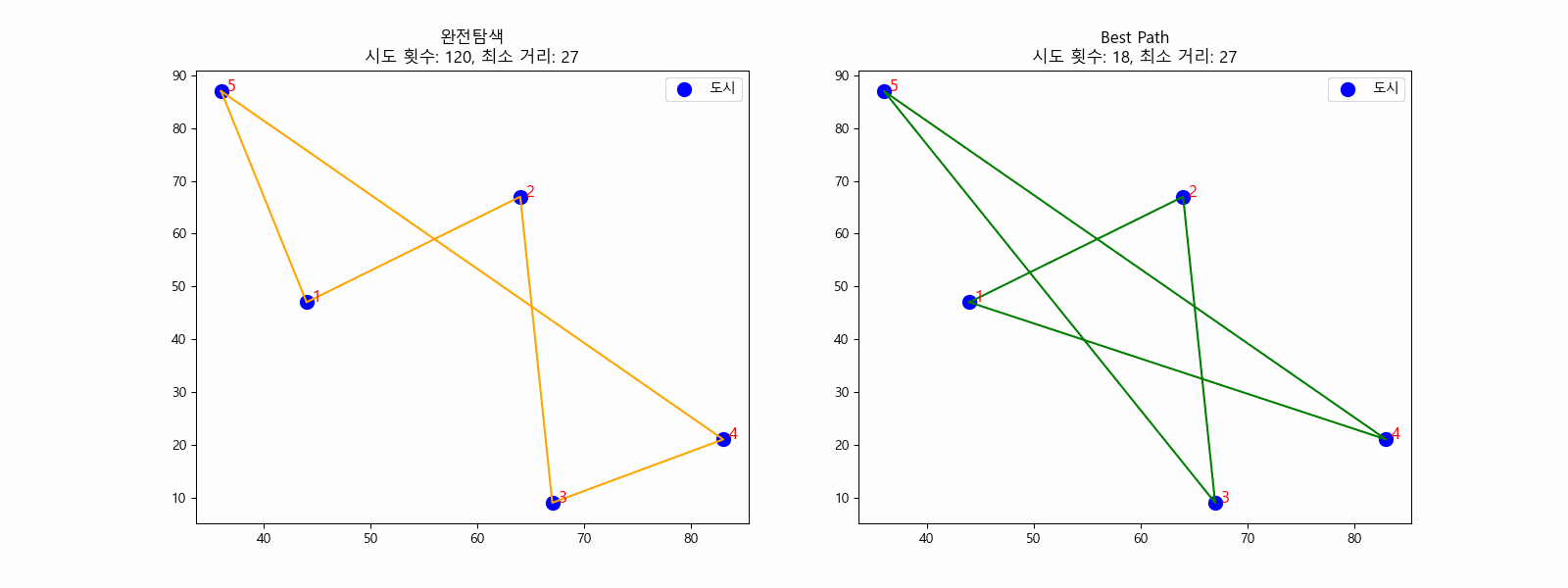
N = 5일 때 최소 거리를 찾는 과정 (완전탐색)

위의 그림과 같이 1 - 5까지 5개 도시가 있고 가중치가 있는 간선으로 이어져 있을 때, 사이클이 있는 최단 경로를 찾기 위해서 먼저 모든 가능한 경로를 구하고 그 중 길이의 최소값만을 택하는 방법을 생각할 수 있습니다. 완전탐색이죠. 가장 확실한 방법이지만, 그만큼 시간복잡도가 큰 방법입니다. 도시의 수가 N개로 늘어나면 시간복잡도는 O(N!)이 됩니다. N = 10일 때 경우의 수는 약 36만 가지, N = 11일 때 경우의 수는 약 4천만 가지입니다.

코드

어쨌든 모든 경우의 수를 탐색하기 위해서는 dfs가 적절할 것으로 보입니다. 코드를 작성하면 다음과 같습니다.

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

/**
 * 외판원 순회 - 완전 탐색 알고리즘
 */
public class Main {
    static int N;
    static int[][] weight; // 각 도시로 가는 가중치 weight[a][b] -> a도시에서 b도시로 가는 비용
    static int answer = Integer.MAX_VALUE; // 최소 거리를 구하기 위해 INF 세팅

    public static void main(String[] args) throws IOException {
        // 입력
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        N = Integer.parseInt(br.readLine());
        weight = new int[N][N];

        StringTokenizer st;
        for (int i = 0; i < N; i++) {
            st = new StringTokenizer(br.readLine());

            for (int j = 0; j < N; j++) {
                weight[i][j] = Integer.parseInt(st.nextToken());
            }
        }

        // 모든 경로를 재귀적으로 탐색하기 위해 dfs 로직 호출
        dfs(0, 0, 1);

        System.out.println(answer);
    }

    /**
     * currentCity - 현재 도착해있는 도시
     * cost - 지금까지 지나온 도시들의 가중치 합
     * visited - 지금까지 지나온 도시의 비트마스킹
     */
    private static void dfs(int currentCity, int cost, int visited) {
        // Base Case
        if (visited == ((1 << N) - 1)) { // 모든 도시를 지나쳐 왔고
            if (weight[currentCity][0] > 0) { // 다시 시작지점으로 돌아갈 수 있다면
                answer = Math.min(answer, cost + weight[currentCity][0]); // 더 작은 cost로 업데이트
            }
            return;
        }

        // Recursive Case
        for (int nextCity = 0; nextCity < N; nextCity++) { // 다음 탐색할 모든 도시 중
            if (nextCity == currentCity) continue; // (다음 탐색할 도시 == 현재 도시)면 패스
            if ((visited & (1 << nextCity)) > 0) continue; // 이미 탐색한 도시면 패스
            if (weight[currentCity][nextCity] == 0) continue; // 경로가 존재하지 않으면 패스

            // dfs 재귀적으로 호출
            dfs(nextCity, cost + weight[currentCity][nextCity], (visited | (1 << nextCity)));
        }
    }
}

코드는 가중치를 저장하기 위한 weight, 최종 답을 저장하기 위한 answer, 그리고 모든 경우의 수를 탐색하기 위한 dfs() 메서드로 단순하게 구성되었습니다.

비트마스킹이 어려운 분들을 위해 visited를 간단히 설명하면 다음과 같습니다.

•

N = 4인 도시들 중에서 visited = 1011₂이라면

임의의 도시를 갔다/안갔다만 구분할 수 있으면 되기 때문에, 위와 같이 표현하면 정수 하나로 각 도시 방문 상태를 나타낼 수 있습니다.

이 완전탐색 풀이는 N ≤ 10정도로 경우의 수가 작을 때만 사용할 수 있는 방법입니다.

Approach B. 분기 한정법(Branch and Bound)

설명

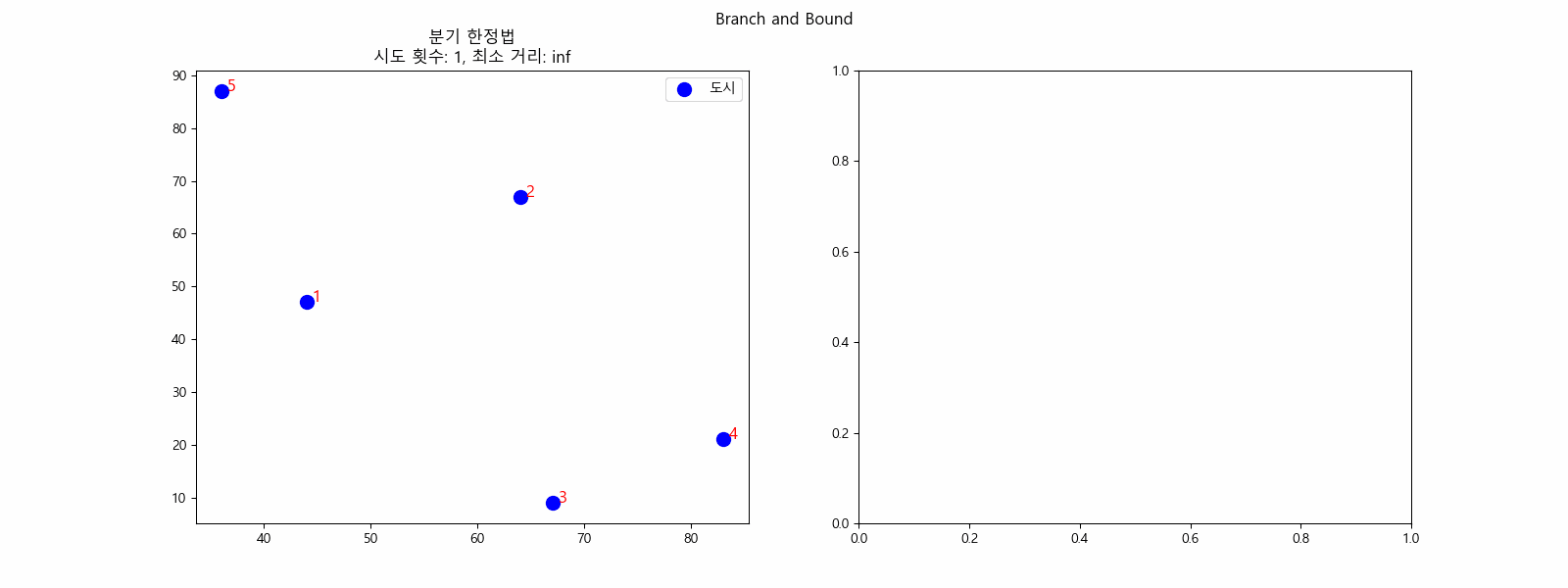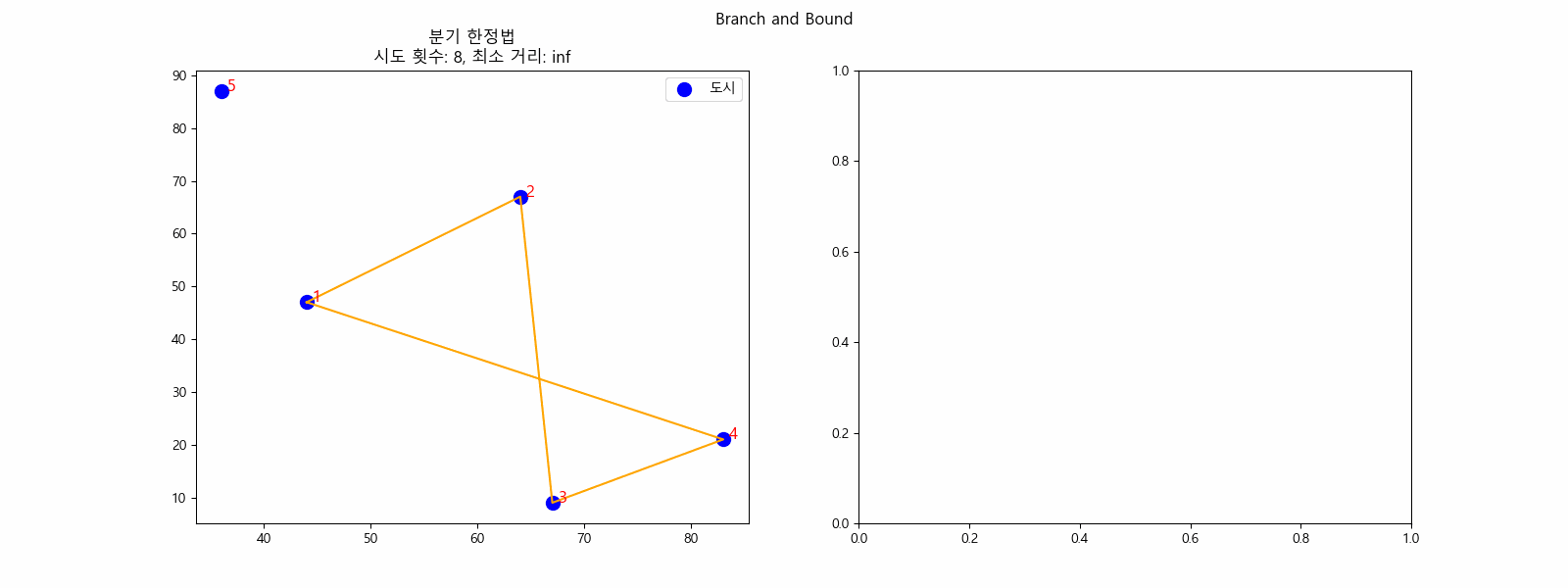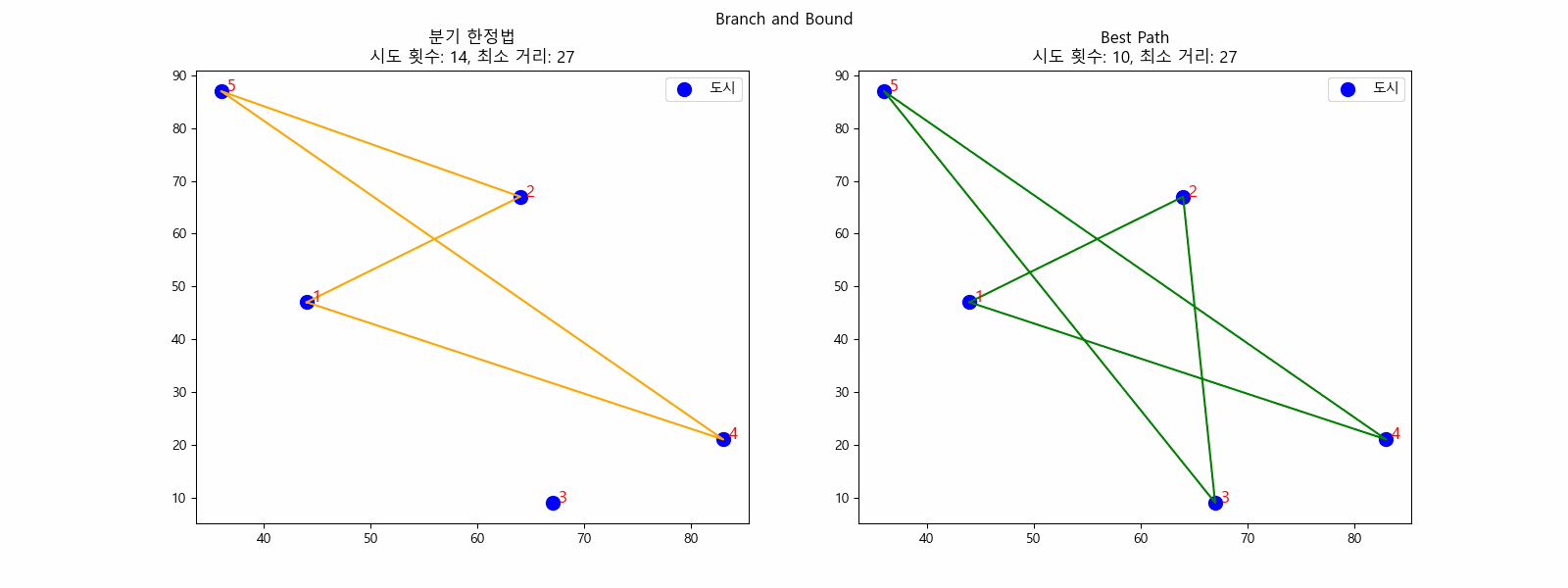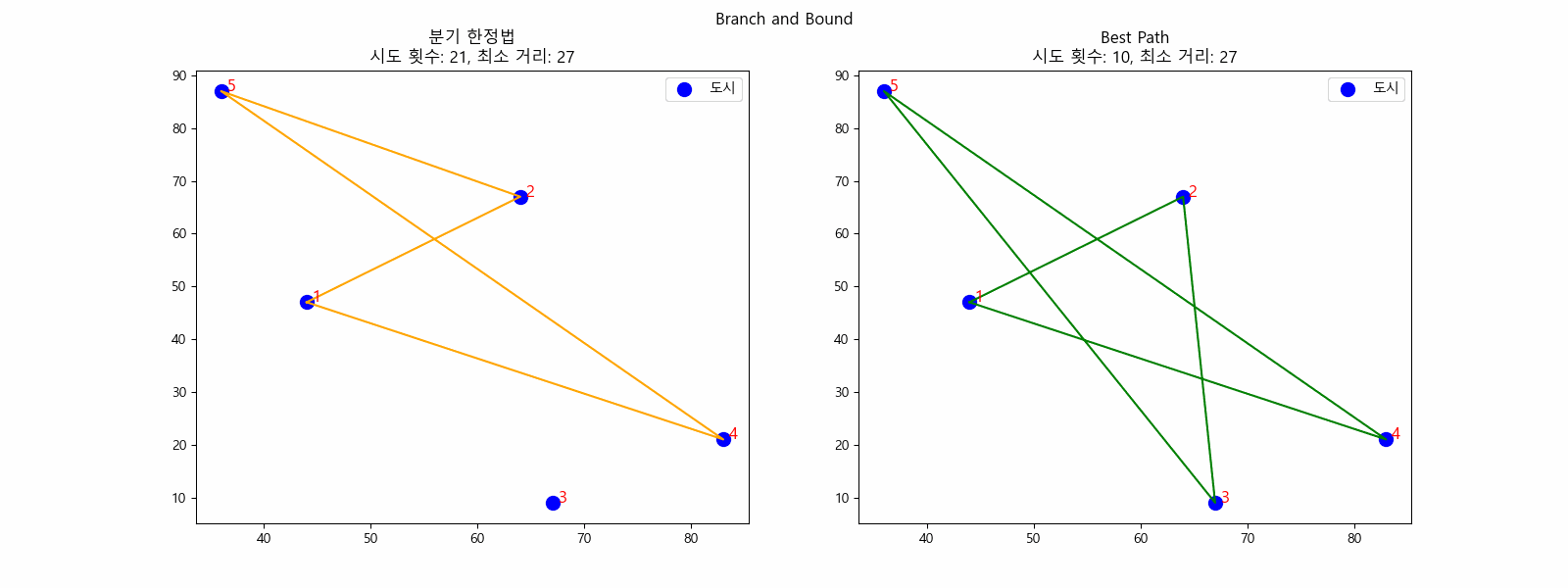
N = 5일때 최소 거리를 찾는 과정(분기 한정법)

앞서 모든 경우의 수를 전부 찾아서 최적의 결과를 찾는 완전탐색은 N이 충분히 작을 경우에만 적용 가능한 한계가 있었습니다. 이 방식을 개선하려면 도시를 탐색할 때 굳이 모든 경로를 가보지 않으면 될 것 같습니다. 임의의 도시에서 다음 방문할 도시를 결정할 때, 어느 경로가 가망이 없는지 미리 알아두고 그 도시는 방문할 후보에서 제외한다면 훨씬 효율적이겠죠. 여기서 분기 한정법이 사용됩니다.

분기 한정법은 모든 후보를 놓고 최적화 할 수치의 상한 혹은 하한 경계(Bound)를 추정해 가망이 없는 경로, 즉 최적의 답으로 이어질 수 없는 경로를 가지치기(Pruning)해 나가는 방법입니다. 제거한 경로에서 파생되는 경로를 살펴보지 않으므로 불필요한 시간 소모를 줄일 수 있습니다.

외판원 순회 문제에서는 전체 이동 거리가 가장 짧은 경로를 찾는 것이 목표입니다. 따라서 하한 경계를 추정해야 합니다. 하한 경계는 해당 경로가 실제로 존재하지 않더라도 경로에 대해서 이론적으로 가능한 최소값을 제공합니다.

예를 들어 이미 몇 개의 경로를 살펴본 후 거리가 30인 경로를 찾았다고 생각할게요. 하지만 확실한 답을 찾으려면 또 다른 경로를 살펴봐야 합니다. 이때 살펴볼 경로의 하한 경계가 35라면(아직은 방문해서 실제 이동 거리가 얼마나 되는지, 경로가 있긴 한건지 확인하진 않았지만 이 경로는 최소한 35 이상의 값을 가진다는 것을 안다면) 굳이 가볼 필요가 없겠죠? 이렇게 하면 불필요한 계산을 방지하고 최적의 솔루션을 찾는 속도가 빨라질 수 있습니다.

이제 실제 가중치가 있는 예제를 가지고 분기 한정법에 따라 하한 경계를 구하고, 문제를 풀어봅시다.

각각의 도시로 가는 경로의 길이

1번 도시에서 자기 자신을 제외하고 다른 도시로 가는 최소 거리는 3번 도시로 가는 4입니다. 그리고 2번 도시에서 자기 자신을 제외하고 다른 도시로 가는 최소 거리는 3번 혹은 5번 도시인 7입니다. 이렇게 각 도시에서 갈 수 있는 최소 경로를 모두 더하면 4 + 7 + 4 + 2 + 4 = 21이 됩니다. 어떤 경로라도 이 경로보다는 최소한 길겠죠. 이것이 초기 하한(lower bound)입니다.

이제 분기 한정법에서는 우선순위 큐(Priority Queue)를 사용해서 하한이 가장 낮은 순서대로 가능한 경로를 탐색하기 시작합니다. 과정은 다음 그림과 같습니다.

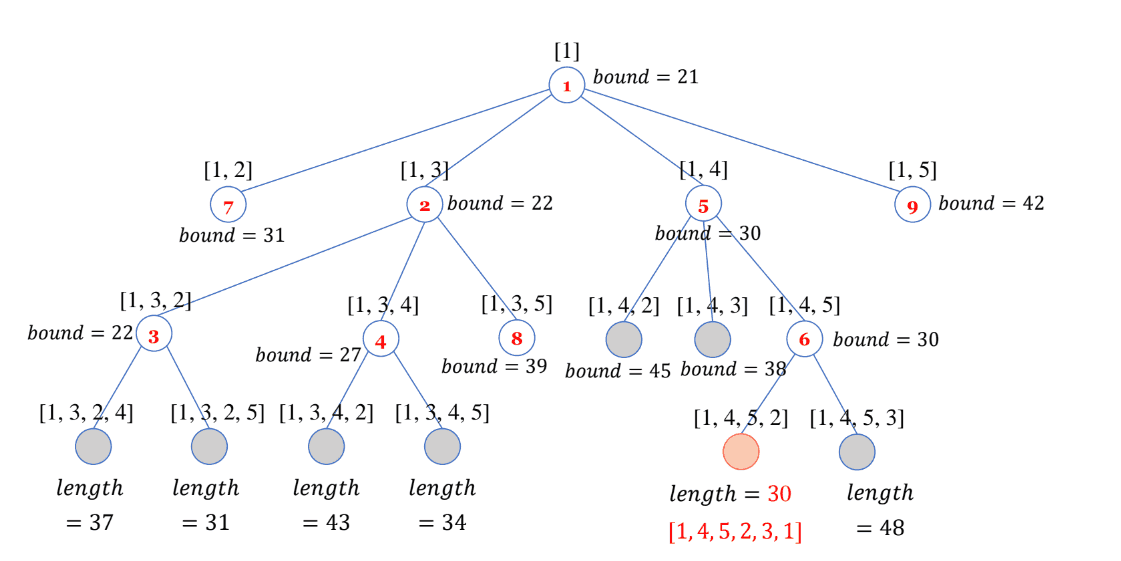
상태 공간 트리 (State-Space Tree)

초기 1번 도시에서 시작합니다. 이 노드를 Node 1이라고 하겠습니다. Node 1에서 갈 수 있는 2, 3, 4, 5번 도시의 bound를 각각 구합니다. 초기 하한이 21이었으니 2번 도시를 방문한다면 bound는 (초기 하한) - (1번 도시에서 갈 수 있는 최소 경로) + (1번 도시에서 2번 도시로 가는 경로)가 되겠네요. 즉, 21 - 4 + 14 = 31입니다. 이처럼 bound를 구하면 가장 정답이 될 가능성이 높은 건 bound가 22인 3번 도시를 방문하는 경우겠네요. 우선순위 큐에 모든 노드를 저장한다면 다음으로 방문하는 건 3번 도시입니다. 이를 Node 2 라고 하겠습니다.

이러한 과정을 반복합니다. 그럼 최종적으로 Node 3에서 마지막 도시인 4, 5번 도시를 각각 방문하면 length를 산출할 수 있습니다. 이 때 가장 짧은 length는 1-3-2-5 도시 순서로 방문하는 31입니다. 이 length는 정답이 될 수 있는 후보로, 가지치기를 하기 위한 중요한 정보입니다

다음으로 가장 작은 bound인 Node 4 를 탐색하고 2번 도시, 5번 도시를 방문해 length를 산출합니다. 43, 34로 현재까지는 31이 정답 후보입니다.

다음으로 가장 작은 bound인 Node 5 를 탐색합니다. 정답 후보가 아직 31이기 때문에 유망한 노드입니다. 4번 도시에서 2, 3, 5번 도시로 갔을 때 bound를 계산하면 각각 45, 38, 30입니다. 45, 38은 이미 정답 후보인 31보다 크기 때문에 가망이 없습니다. 제외합니다. 5번 도시로 가는 Node 6 로 갑니다.

Node 6 에서 2번 도시를 방문했을 때 기존 정답 후보보다 작은 30이 나왔습니다. 업데이트합니다.

다음으로 우선순위 큐에서 Node 7 , Node 8 , Node 9 를 뽑지만 전부 정답 후보인 30보다 bound가 커서 가망이 없습니다.

최종적으로 정답 후보인 30이 정답이 됩니다.

이처럼 정답 후보보다 큰 bound를 가진 노드를 가지치기해 그 노드에서 파생되는 경로를 가지 않음으로써 시간 소모를 줄이는 방법입니다. 모든 경우의 수를 전부 탐색하는 완전탐색보다 확실히 효율적인 방법이죠? 코드로 보면 다음과 같습니다.

코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.PriorityQueue;
import java.util.Queue;
import java.util.StringTokenizer;

/**
 * 외판원 순회 - 분기 한정법 알고리즘
 */
public class Main {
    static int N;
    static int[] pathOfTheLowest; // bound를 계산할 때 각 도시에서 갈 수 있는 최소 거리를 캐싱
    static int[][] weight; // 각 도시로 가는 가중치 weight[a][b] -> a도시에서 b도시로 가는 비용
    static int answer = Integer.MAX_VALUE; // 최소 거리를 구하기 위해 INF 세팅

    /**
     * 상태공간트리(State-Space Tree) 노드
     */
    static class Node implements Comparable<Node> {
        int currentCity, level, visited, bound, length;

        public Node(int currentCity, int level, int visited, int bound, int length) {
            this.currentCity = currentCity; // 현재 도시
            this.level = level; // 몇 개의 도시를 방문한 상태인지
            this.visited = visited; // 어떤 도시를 방문했는지
            this.bound = bound; // 하한 경계
            this.length = length; // 현재까지 방문한 경로
        }

        // 우선순위큐에서 낮은 경계부터 뽑기 위해 오버라이드
        @Override
        public int compareTo(Node o) {
            return Integer.compare(bound, o.bound);
        }
    }

    public static void main(String[] args) throws IOException {
        // 입력
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        N = Integer.parseInt(br.readLine());
        weight = new int[N][N];
        pathOfTheLowest = new int[N];

        StringTokenizer st;
        for (int i = 0; i < N; i++) {
            st = new StringTokenizer(br.readLine());

            for (int j = 0; j < N; j++) {
                weight[i][j] = Integer.parseInt(st.nextToken());
            }
        }

        // 분기 한정법 로직 호출
        branchAndBound();

        System.out.println(answer);
    }

    private static void branchAndBound() {
        Queue<Node> pq = new PriorityQueue<>(); // 가장 작은 경계를 가진 노드를 호출하기 위해 우선순위큐 사용

        int initialBound = getInitialBound(); // 초기 최소 경계를 설정

        pq.add(new Node(0, 0, 1, initialBound, 0));

        while (!pq.isEmpty()) {
            Node node = pq.poll();

            if (node.bound > answer) continue; // 노드의 하한이 이미 현재 정답 후보보다 크면 가망이 없으므로 패스

            int currentCity = node.currentCity;
            int visited = node.visited;
            int bound = node.bound;
            int level = node.level;
            int length = node.length;

            for (int nextCity = 0; nextCity < N; nextCity++) {
                if ((visited & (1 << nextCity)) > 0) continue; // 이미 방문한 도시면 패스
                if (weight[currentCity][nextCity] == 0) continue; // 경로가 없으면 패스

                // 다음 도시를 거쳐서, 시작점으로 돌아오면 사이클이 형성될 때는
                if (node.level == N - 2) {
                    if (weight[nextCity][0] > 0) { // 그 경로가 있다면
                        // 경로를 구하고
                        int path = node.length + weight[currentCity][nextCity] + weight[nextCity][0];

                        // 업데이트
                        answer = Math.min(answer, path);
                    }

                    continue;
                }

                int newBound = getBound(currentCity, nextCity, bound); // 경계 업데이트

                Node newNode = new Node(
                        nextCity,
                        level + 1,
                        visited | (1 << nextCity),
                        newBound,
                        length + weight[currentCity][nextCity]
                );

                if (newBound < answer) { // 경계가 현재 정답보다 작을 때만
                    pq.add(newNode); // 우선순위큐에 추가
                }
            }
        }
    }

    private static int getBound(int currentCity, int nextCity, int bound) {
        return bound - pathOfTheLowest[currentCity] + weight[currentCity][nextCity];
    }

    private static int getInitialBound() {
        int bound = 0;

        for (int startCity = 0; startCity < N; startCity++) { // 각 도시에서
            int minWeight = Integer.MAX_VALUE; // 다른 도시로 가는 최솟값을 찾기 위해 INF 초기화

            // 다른 도시로 갈 때 최소 경로를 찾기
            for (int endCity = 0; endCity < N; endCity++) {
                if (startCity == endCity) continue; // 시작 도시 == 도착 도시면 패스
                minWeight = Math.min(minWeight, weight[startCity][endCity]);
            }

            pathOfTheLowest[startCity] = minWeight; // 각 도시에서 가는 최소 경로 저장
            bound += minWeight; // 최소 경로만을 더하기
        }

        return bound;
    }
}

상태 공간 트리의 상태를 관리할 Node 클래스를 정의합니다. 이 클래스는 현재 어느 도시에 있는지 currentCity , 몇 개의 도시를 방문한 상태인지 level, 어떤 도시들을 방문한 상태인지 visited , 현 상황에서 계산한 하한 경계 bound, 그리고 현재까지 지나온 길을 다 더한 length 의 상태들을 관리합니다.

다음으로 분기한정법 로직을 수행하는 branchAndBound() 메서드를 봅시다. 가장 먼저 우선순위 큐를 초기화하고, 시작 위치에서 하한 경계를 계산하기 위해 getInitialBound() 메서드를 호출해 initialBound 를 계산합니다. 로직은 단순히 이중반복문을 통해 각 도시에서 다른 도시로 갈 때 최소 경로를 찾아서 모두 더한 뒤 리턴합니다.

그리고 이 정보를 바탕으로 Node 인스턴스를 만들어 우선순위 큐에 집어넣은 후 반복적으로 호출하면서 bound가 가장 낮은 Node부터 계산합니다.

이 때, Node의 bound가 이미 정답 후보인 answer 보다 크다면(node.bound > answer) 제외해야겠죠.

이처럼 가망이 없는 경로를 가지치기해 시간을 절약하는 장점에도 불구하고, 분기 한정법은 N이 클수록 계산량이 급증할 수 있습니다. 또, 절대 답이 될 수 없는 가지를 쳐내는 것에 불과하기 때문에 실제로 얼마나 시간이 절약될지 장담할 수 없고, 우선순위 큐에 저장해야 할 노드의 수도 늘기 때문에 공간적으로도 불리해질 수 있습니다.

그렇다면 왜 알아야 할까요? 그건 이후 TSP를 근사해서 풀기 위한 방식의 기초가 되기 때문입니다.

어쨌거나 분기 한정법으로는 예시 문제인 백준의 외판원 순회 문제를 풀기 힘듭니다. 조건이 N ≤ 16이므로 시간적, 공간적으로 확정적인 방법이 아니면 힘들겠네요. 그래서 동적 프로그래밍으로 풉니다.

Approach C. 동적 프로그래밍 (DP)

동적 프로그래밍은 큰 문제를 작게 나누어 재귀적으로 풀고, 이미 계산된 결과를 저장해두어 중복 계산을 줄이는 방법입니다. 특히 이러한 최적화 문제를 풀 때 유용해요.

외판원 문제에서 동적 프로그래밍은 메모이제이션(Memoization) 기법과 함께 사용됩니다. 이 방법에서는 모든 경로를 탐색하지 않고, 현재까지 방문한 도시의 집합과 마지막으로 방문한 도시를 기준으로 최적의 경로를 계산합니다.

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;

/**
 * 외판원 순회 - 동적 계획법
 */
public class Main {
    static int N;
    static int[][] weight;
    static int[][] dp;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        N = Integer.parseInt(br.readLine());
        weight = new int[N][N];
        dp = new int[N][1 << N];

        StringTokenizer st;
        for (int i = 0; i < N; i++) {
            Arrays.fill(dp[i], Integer.MAX_VALUE); // dp 배열 최댓값으로 초기화
        }

        dp[0][1] = 0; // 0번 도시에서 시작, 0번 도시를 방문 가능 상태로 설정 (초기 비용 0)

        for (int i = 0; i < N; i++) {
            st = new StringTokenizer(br.readLine());

            for (int j = 0; j < N; j++) {
                weight[i][j] = Integer.parseInt(st.nextToken());
            }
        }

        // 모든 방문 상태를 탐색
        for (int visited = 1; visited < (1 << N); visited++) { // 방문 상태를 1부터 2^N - 1까지 탐색
            for (int currentCity = 0; currentCity < N; currentCity++) { // 현재 도시를 설정
                // 현재 도시가 방문할 경로 visited에 포함되어 있지 않다면 패스
                if ((visited & (1 << currentCity)) == 0) continue;

                // 다음 방문할 도시 찾기
                for (int nextCity = 0; nextCity < N; nextCity++) {
                    // 이미 방문한 도시거나, 경로가 없을 경우 패스
                    if ((visited & (1 << nextCity)) != 0 || weight[currentCity][nextCity] == 0) {
                        continue;
                    }

                    // dp값이 유효하지 않으면 패스(앞선 연산에서 경로가 없어서 업데이트가 안됐던 것)
                    if (dp[currentCity][visited] == Integer.MAX_VALUE) continue;

                    // 다음 도시를 방문한 상태의 최소 비용 업데이트
                    dp[nextCity][(visited | (1 << nextCity))] =
                            Math.min(
                                    dp[nextCity][visited | (1 << nextCity)], // 기존 값
                                    dp[currentCity][visited] + weight[currentCity][nextCity] // 현재 도시에서 다음 도시로 이동 비용 합산
                            );
                }
            }
        }

        int answer = Integer.MAX_VALUE; // 최종적으로 최소 비용을 저장할 변수

        // 모든 도시를 방문한 상태에서 시작 도시로 돌아가는 경로의 최소 비용 계산
        for (int i = 1; i < N; i++) { // 1번 도시부터 N - 1번 도시까지 확인
            // 시작 도시로 갈 수 있는 경로가 있고, 비용이 유효하다면
            if (weight[i][0] != 0 && dp[i][(1 << N) - 1] != Integer.MAX_VALUE) {
                answer = Math.min(answer, dp[i][(1 << N) - 1] + weight[i][0]); // 최소 비용 업데이트
            }
        }

        System.out.println(answer);
    }
}

참고자료

•

https://gazelle-and-cs.tistory.com/18

•

https://ko.wikipedia.org/wiki/분기_한정법

외판원 문제란?
문제 풀기
Approach A. 완전탐색(DFS)
설명
코드
Approach B. 분기 한정법(Branch and Bound)
설명
코드
Approach C. 동적 프로그래밍 (DP)
참고자료